modulo lll
semana 3
DISTRIBUCION BINOMIAL
la distribución binomial es un modelo estadístico que permite calcular la probabilidad de obtener un numero determinado de éxito en un numero determinado de éxitos en un numero fijo de pruebas, donde:
- cada prueba tiene solo dos posibles resultados (éxito o fracaso).
- la probabilidad de éxito es la misma en cada intento.
- los intentos son independientes entre si.
- en cada ensayo, experto o prueba solo son posibles dos resultados (éxito o fracaso).
- la probabilidad del éxito ha de ser constante. esta se representa mediante la letra p. la probabilidad de salga cara al lanzar una moneda es 0,5 y esta es constante dado que la moneda no cambia en cada en cada experimento y las probabilidades de sacar cara son constantes.
- el resultado obtenido en cada experimento es independiente del anterior . por lo tanto, lo que ocurra en cada experimento no afecta a los siguientes.
3) Función de probabilidad binomial (fórmula)
Para un experimento binomial, sea p la probabilidad de “éxito” y 1-p la probabilidad de un “fracaso” en un solo ensayo; entonces la probabilidad de obtener x éxitos en n ensayos, está dada por la función de probabilidad f(x):

Siendo el coeficiente binomial o número combinatorio:
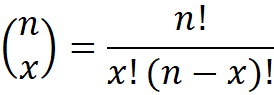
Por eso, en algunos libros encontrarás la función de probabilidad binomial f(x) con el coeficiente binomial ya incorporado y presentada de la siguiente manera:

¿Cuál de las formas es la mejor? Eso ya depende de lo que diga tu corazón, pero recuerda que el resultado es el mismo.
La función de probabilidad binomial se aplica a cualquier experimento binomial. Si una situación demuestra las propiedades de un experimento binomial y se conocen los valores de n y p, se puede usar la ecuación de arriba para calcular la probabilidad de x éxitos en n ensayos. Recuerda, antes de usar la fórmula de probabilidad binomial, siempre verifica que te encuentres ante un experimento binomial.
4) Media, varianza y desviación estándar de la distribución binomial
La media, la varianza y la desviación estándar se pueden encontrar con estas fórmulas:
Media:

Varianza:

Desviación estándar:

5) Ejemplos
La probabilidad de que a un cliente nuevo le guste la matehamburguesa de Jorge es de 0,8. Si llegan 5 clientes nuevos a la cafetería, ¿cuál es la probabilidad de que solo a 3 de ellos les guste la matehamburguesa?
Solución:
Antes de aplicar la fórmula, verificamos que se trate de un experimento binomial. Para ello, tiene que cumplir con las 4 condiciones que mencionamos arriba. Efectivamente, se trata de un experimento binomial.
En este caso, vamos a centrarnos en los clientes a los que les gusta esta hamburguesa, por ello diremos que:
X = número de clientes nuevos de 5 a los que les gusta la matehamburguesa
Entonces consideramos un éxito si al cliente le gusta esta hamburguesa.
Aplicaremos la fórmula binomial:

Ahora colocamos los valores de n, k y p. Recuerda que n es el número de ensayos, k el número de éxitos y p la probabilidad de éxito.

Reemplazamos estos valores en la fórmula:






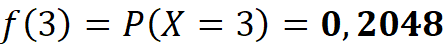
La respuesta sería 0,2048.
Recuerda que X, nuestra variable aleatoria, es el número de clientes nuevos de 5 a los que les gustan las hamburguesas de Jorge. Aunque el problema no lo pide, vamos a elaborar la tablita de distribución de probabilidad. Para calcular todas las probabilidades, usaré la misma fórmula de arriba.
Ejemplo 2
De todas las flores plantadas por una empresa de jardinería, el 90% sobrevive. Si se plantan 10 flores ¿cuál es la probabilidad de que 9 o más sobrevivan?
Solución:
Antes de aplicar la fórmula, verificamos que se trate de un experimento binomial. Para ello, tiene que cumplir con las 4 condiciones que mencionamos arriba. Efectivamente, se trata de un experimento binomial.
En este caso, vamos a centrarnos en las flores que sobreviven, por ello diremos que:
X = número de flores de 10 que sobreviven
Entonces consideramos un éxito si la flor sobrevive. A las que flores que se mueren, las consideramos como un fracaso.
Aplicaremos la fórmula binomial:

Nos piden calcular la probabilidad de 9 o más sobrevivan.
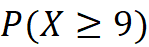
Este problema tiene trampa, porque dado que se plantaron 10 flores, la máxima cantidad de flores que pueden sobrevivir es 10, por lo tanto:

– ¿Y no pueden sobrevivir 11 flores?
– No se puede, porque solo se plantaron 10.
– ¿Y si las flores tienen hijitos bonitos?
– Alumno por favor, tome menos azúcar. Concéntrese y sigamos con la clase.
Ahora colocamos los valores de n, k y p. Recuerda que n es el número de ensayos, k el número de éxitos y p la probabilidad de éxito. En este caso:

Regresamos con la fórmula de arriba:

Vamos a calcular cada probabilidad por separado, empezando con P(X = 9):




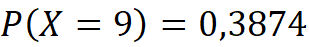
Continuamos con P(X = 10).

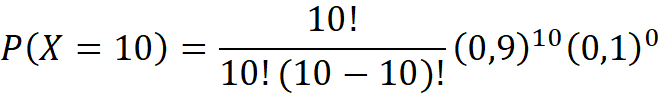




Regresamos con esta fórmula:

Y reemplazamos lo calculado:


Ejemplo 3
Considere un experimento binomial con dos ensayos y p=0,4.
a) Calcular la probabilidad de no obtener ningún éxito.
b) Calcular la probabilidad de obtener al menos 1 éxito.
Solución:
Iniciamos definiendo la variable aleatoria de interés en nuestro experimento binomial:
X = número de éxitos en n ensayos.
x = 0; 1; 2.
El enunciado nos dice que: n = 2 y que p = 0,4; con ello podemos definir la función de probabilidad de X.



a) Calcular la probabilidad de no obtener ningún éxito: P(X = 0).



b) Calcular la probabilidad de obtener al menos 1 éxito.
Aquí nos piden calcular:

Pero:
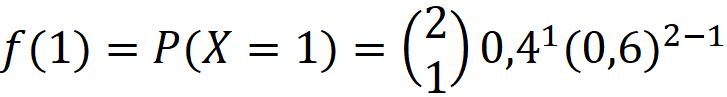

Además:


Reemplazamos:



Esa sería la respuesta: 0,64.
Una forma alternativa de desarrollar el apartado b, sería usando la siguiente
“La suma de las probabilidades para todos los resultados del experimento debe ser igual a 1”.



Pero recuerda que P(X=0) ya lo calculamos en el apartado a, y es igual a 0,36.



